引入
一个班喜欢篮球的有 a 人, 喜欢足球的有 b 人,喜欢乒乓球的有 c 人,请问你至少喜欢一个运动的有多少人?
首先很明显答案不是简单的 a+b+c ,因为可能有人既喜欢足球又喜欢篮球,所以全部加起来会把这些人算重。
我们用集合的思路去考虑:
喜欢篮球,足球,乒乓球的人的集合分别是 A,B,C,则我们要求的实际是 ∣A∪B∪C∣ 。
相比较于∣A∣+∣B∣+∣C∣,答案应该把多算了的∣A∩B∣… 减掉,但是这样就得再把多减掉的∣A∩B∩C∣ 加回来,即:
∣A∪B∪C∣=∣A∣+∣B∣+∣C∣−∣A∩B∣−∣A∩C∣−∣B∩C∣+∣A∩B∩C∣
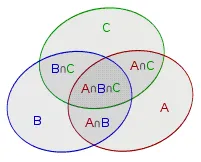
定义
设 U 中 元素有 n 种不同的属性,而第 i 种属性称为 Pi,拥有属性 Pi 的元素构成集合 Si,那么
i=1⋃nSi=m=1∑n(−1)m−1ai<ai+1∑i=1⋂mSai
简单来说就是:奇加偶减
ai<ai+1 表示加和时只计算一次。
补集
更常见的一些情况,当你需要计算一些集合的并的时候,根据德摩根律:
i=1⋂nSi=∣U∣−i=1⋃nSiˉ
你会发现除去减数刚好适用于容斥定理,从而得到:
i=1⋂nSi=∣U∣−i=1⋃nSiˉ=∣U∣−m=1∑n(−1)m−1ai<ai+1∑i=1⋂mSˉai
例题
给定 x,n。求各元素各不相同的集合(a1,a2,...,an)的数量,使得lcm(a1,a2,...,ak)+gcd(a1,a2,...ak)=x. 1≤x,n≤109.
首先能够想到 lcm 一定是 gcd 的倍数,从而 gcd 是 lcm 的因子,也一定是 x 的因子。从而首先枚举 x 的因子 factor, 则 lcm=x−factor, 每个数都是 x 的倍数,所以问题变为满足gcd=1,lcm=factorx−factor 的集合数量。
令 t=factorx−factor , 从而题目转化为:
给定 x,n。求各元素各不相同的集合(a1,a2,...,an)的数量,使得lcm(a1,a2,...,an)=t 且 gcd(a1,a2,...an)=1. 1≤x,n≤109.
考虑将 t 做质因数分解,得到每个质因子的出现次数的集合 S , t=a1∗q1+a2∗q2+...+am∗qm, S={a1,a2,a3,...,am}, m 为最后一个质因子.
当不保证 gcd=1 时
这个时候,考虑这 n 个数的 lcm=t,即只要 t 的每个质因子 qi ,在每个数中,出现次数都不超过 ai 次,即每个因子可以在每个数中出现 0−vi 次,一共能组合出 P=(v1+1)∗(v2+1)∗(v3+1)...∗(vm+1)=∏i∈v(i+1) 种,则方案是CPn 种。
保证 gcd=1 时
考虑这里的方法,此时 U 对应不保证 gcd=1的答案,从而需要考虑原限制的反,即所有gcd=1 时的答案的并集 ⋃i=1nSiˉ.
考虑如何保证答案的gcd=1,即保证每个数都一定选取一个指定的因子即可。
所以我们考虑枚举一个 m 位的二进制数, 哪一位为 1 代表对应那一位的质因子被每个数都选取了。这个时候考虑容斥,你会发现,当刚好有奇数个质因子全被选取的时候,就加上,对应偶数个就减去,刚好对应奇加偶减。
答案的统计也要稍作修改,对应的一定全被选取的那一个质因子的可能性将会从 i+1 次 变为 i 次(因为一定被选中一次)。
此时统计的答案即为当 lcm 为 t 的因子,且 gcd 为 1 的集合数量。
保证 lcm=t 时
接下来用完全同样的方法考虑lcm 恰好等于 t 的情况:
- 考虑原限制的反:所有 lcm=t 时的答案的并集
- 考虑如何保证所有答案 lcm=t :保证对于每一个数,质因子出现次数的最大值都小于对应的 vi,即保证这个质因子不被选取 vi 次
你会发现这就和前半部分一模一样了,这一次二进制数位为1就代表对应的那一位的质因子一定没有被选取到 vi 次,从而对应的因子可选取次数又要 −1。
将两次容斥结合在一起,就能得出最后的方案数。
代码参考
未完待续…
